Despite their remarkable fluency, large language models can produce confident yet incorrect outputs—so-called confabulations, a subset of hallucinations that involve false statements which are sensitive to random seed variations. In “Detecting Hallucinations in Large Language models using Semantic Entropy” (Farquhar et al., 2024), they introduce “semantic entropy”, a metric that captures a model’s uncertainty about the meaning of its responses. In this post, I explore how to use it to both detect and reduce such failures through a variety of methods including targeted steering interventions.
1. Background
Let $X$ be the set of language sequences and $P$ a model’s probability distribution over $X$. Given some context $x$, one way to estimate the model’s uncertainty about its response $y$ is via (naive) predictive entropy ($PE$), defined as:
\[PE = -\sum_y P(y|x) \log P(y|x).\]To account for the fact that different sequences may express the same underlying meaning—for instance, “It is Paris” and “Paris” are semantically equivalent—semantic entropy ($SE$) clusters responses $y_n$ into semantic equivalence classes $C_k$ and then measures entropy across these classes by summing over the response probabilities:
\[\begin{align*} SE &= -\sum_{C_k} P(C_k|x) \log P(C_k|x) \\ &= -\sum_{C_k} \left( \sum_{y_n \in C_k} P(y_n|x) \right) \log \left( \sum_{y_n \in C_k} P(y_n|x) \right). \end{align*}\]In practice, estimating (both naive and semantic) entropy requires generating multiple model responses (typically 5 to 10) at higher temperature settings to capture meaningful variation in responses. To group responses into classes, Farquhar et al. relied on the notion of bidirectional entailment (i.e., $x$ implies $x’$ and vice versa for $x, x’ \in X$); they estimate bidirectional entailment using an LLM as a judge.
2. Experiments
To investigate semantic entropy’s potential in reducing confabulations, I conducted a few quick experiments (all using LLaMA-7B on a subset of 500 examples from the TriviaQA dataset).
2.1. Semantic Equivalence and Embedding Structure
To begin, I examined whether semantic equivalence classes corresponded to structure in the model’s embedding space. For an input question with high semantic entropy, I sampled 50 answers and visualized their last-layer embeddings; as expected, sequences grouped into the same semantic class (of which there were 17) tended to cluster closely in the embedding space, suggesting that semantic equivalence classes reflects embedding space structure.
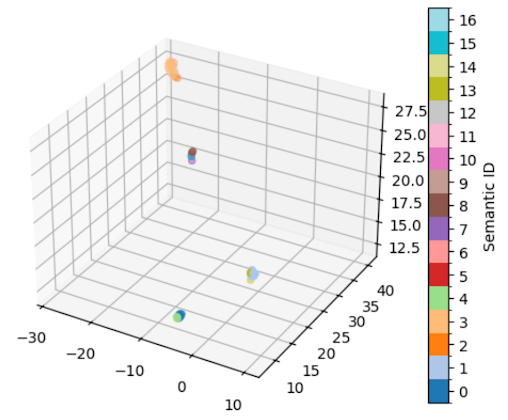
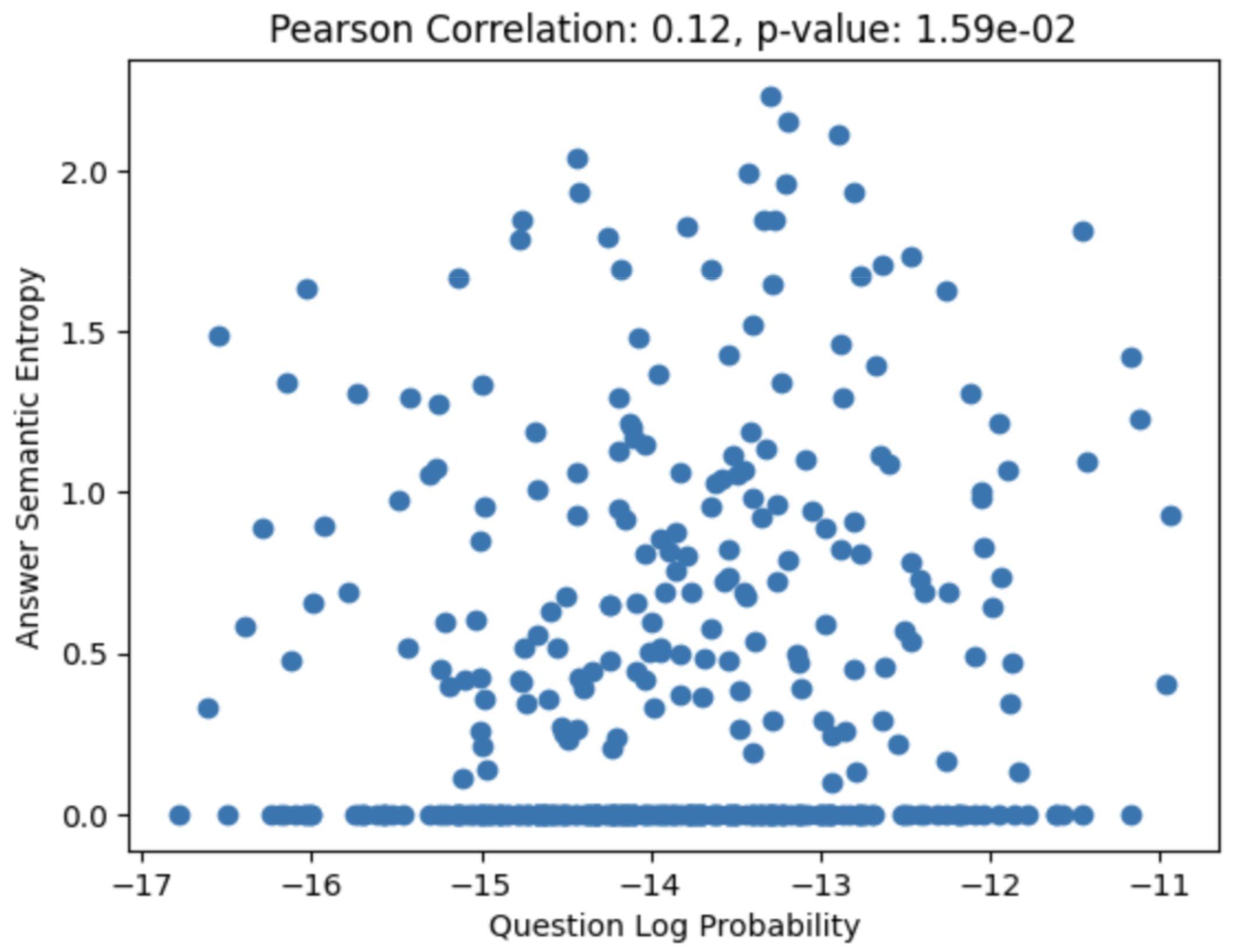
2.2. Question Probability and Response Semantic Entropy
Intuitively, one might expect the model to be more prone to confabulation on inputs that are underrepresented in its training distribution. To test this, I estimated the log-probability of each question and examined its correlation with the semantic entropy of the corresponding answers, but surprisingly, there was little to no correlation between the two.
2.3. Semantic Entropy Linear Probe
Given that semantic entropy is expensive to compute, prior work (Kossen et al., 2024) has proposed training a linear probe to predict it directly from internal embeddings. I replicated this approach and found that while such probes outperform baseline heuristics, their predictive power still falls short of using true semantic entropy.
2.4. Semantic Entropy Steering Vector
I also explored whether semantic entropy could be used to steer the model away from confabulations. I constructed a semantic entropy steering vector by subtracting the mean embedding of low-entropy responses from that of high-entropy ones. The model’s final-layer activations were then adjusted via:
\[a' = a - \lambda v_{SE},\]where $a$ are the original activations, $\lambda$ is a tunable scaling factor, and $v_{SE}$ is the steering vector. As $\lambda$ increased, the model began to refuse to answer (producing a stop token), and beyond a certain threshold, its responsese became increasingly incoherent. Measuring accuracy and refusal rate across the 500-example subset revealed a kind of “phase transition” in behavior as $\lambda$ varied.
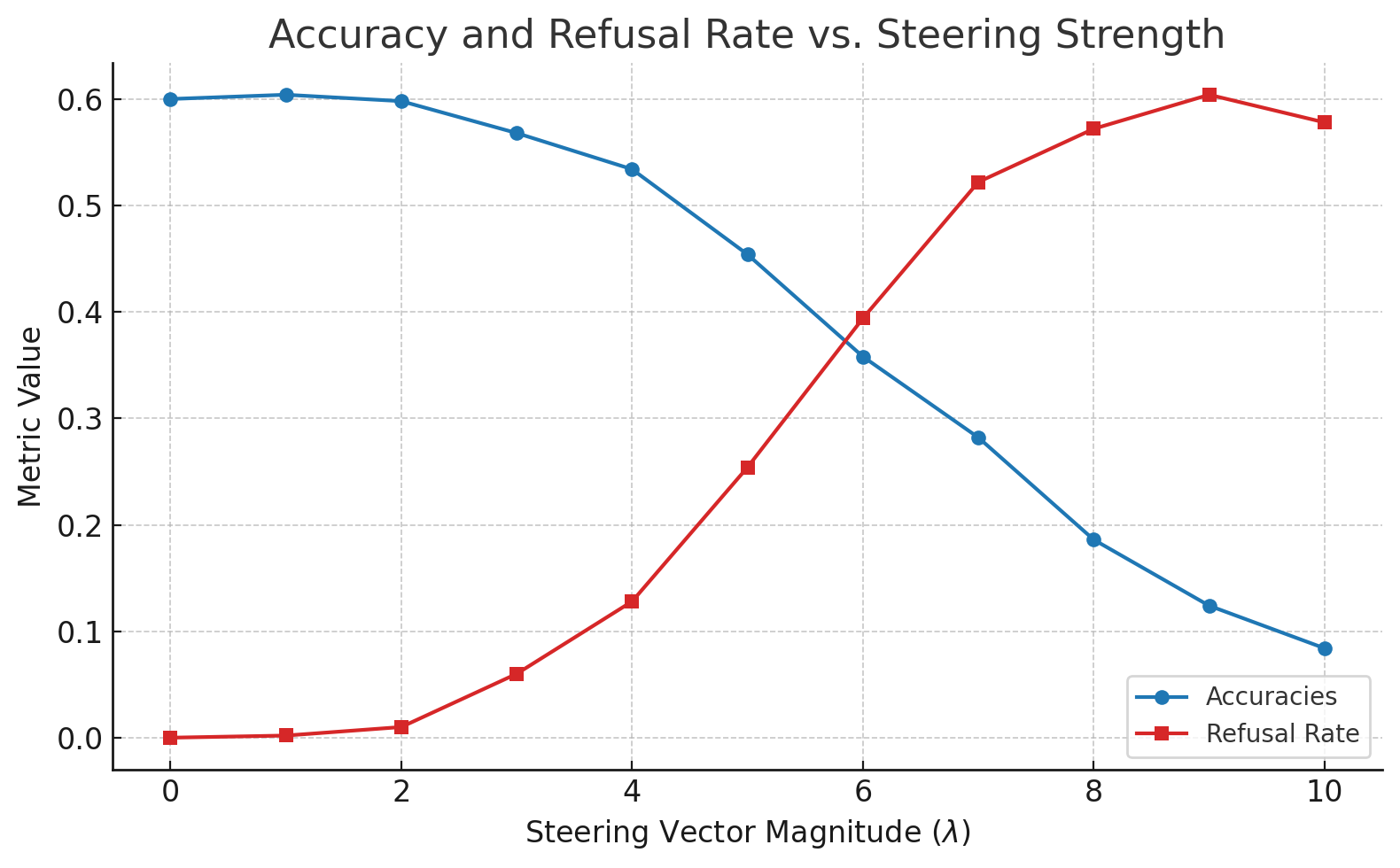
3. Future Directions
Several avenues remain for deeper investigation:
- Expand the experiments to the full 15,000 examples in the TriviaQA dataset.
- Compute and log semantic entropy for all examples to enable a broader statistical analysis.
- Re-estimate the steering vector using the full labeled dataset and explore more nuanced ways to group responses into semantic classes.
- Experiment with applying the steering vector at other layers (or across multiple layers) of the model.
- Conduct a more fine-grained search over the magnitude parameter $\lambda$ to better characterize the transition dynamics and optimal operating points.